“Celtic Knots on Einstein Lattice” by Ben

I recently posted about doing Celtic Knots on a Hexagonal lattice ( https://www.lesswrong.com/posts/tgi3iBTKk4YfBQxGH/celtic-knots-on-a-hex-lattice ).

There were many nice suggestions in the comments. @Shankar Sivarajan suggested that I could look at a Einstien lattice instead, which sounded especially interesting. ( https://en.wikipedia.org/wiki/Einstein_problem . )

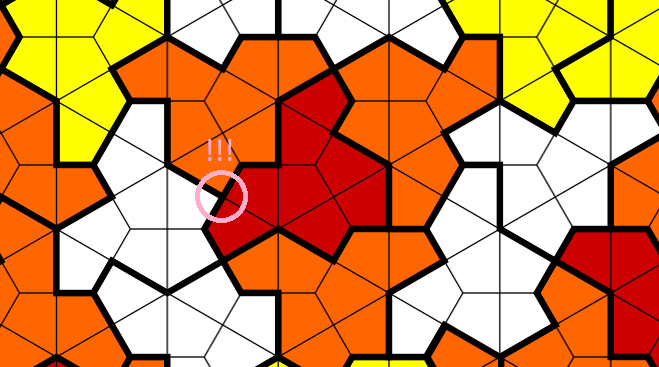
The idea of the Einstein tile is that it can tile the plane (like a hexagon or square can), but it does so in a way where the pattern of tiles never repeats.

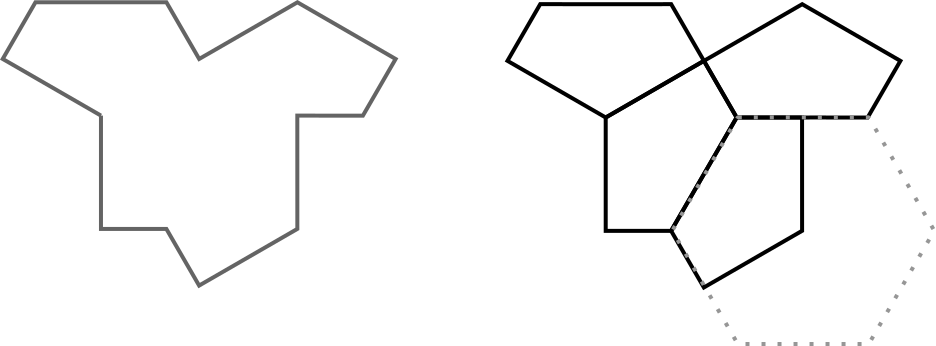
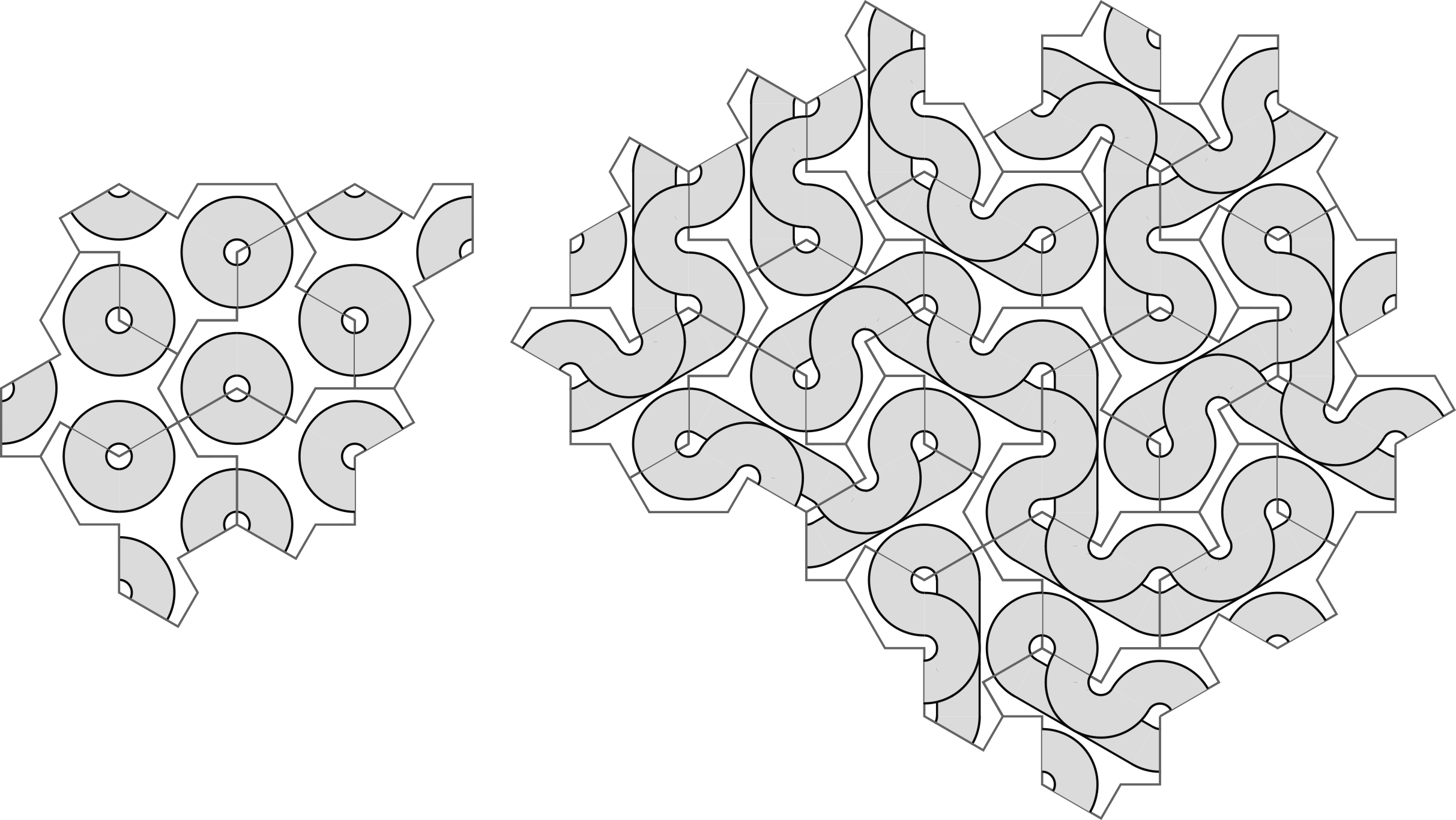
The tile I took from Wikipedia looks like this:

On the left is the full tile. On the right is a way of decomposing it into four-thirds of a hexagon.

For some reason I think of it as a lama. On the left top is its head, facing left. On tie right top its its tail. The squarish bit coming down is the legs.

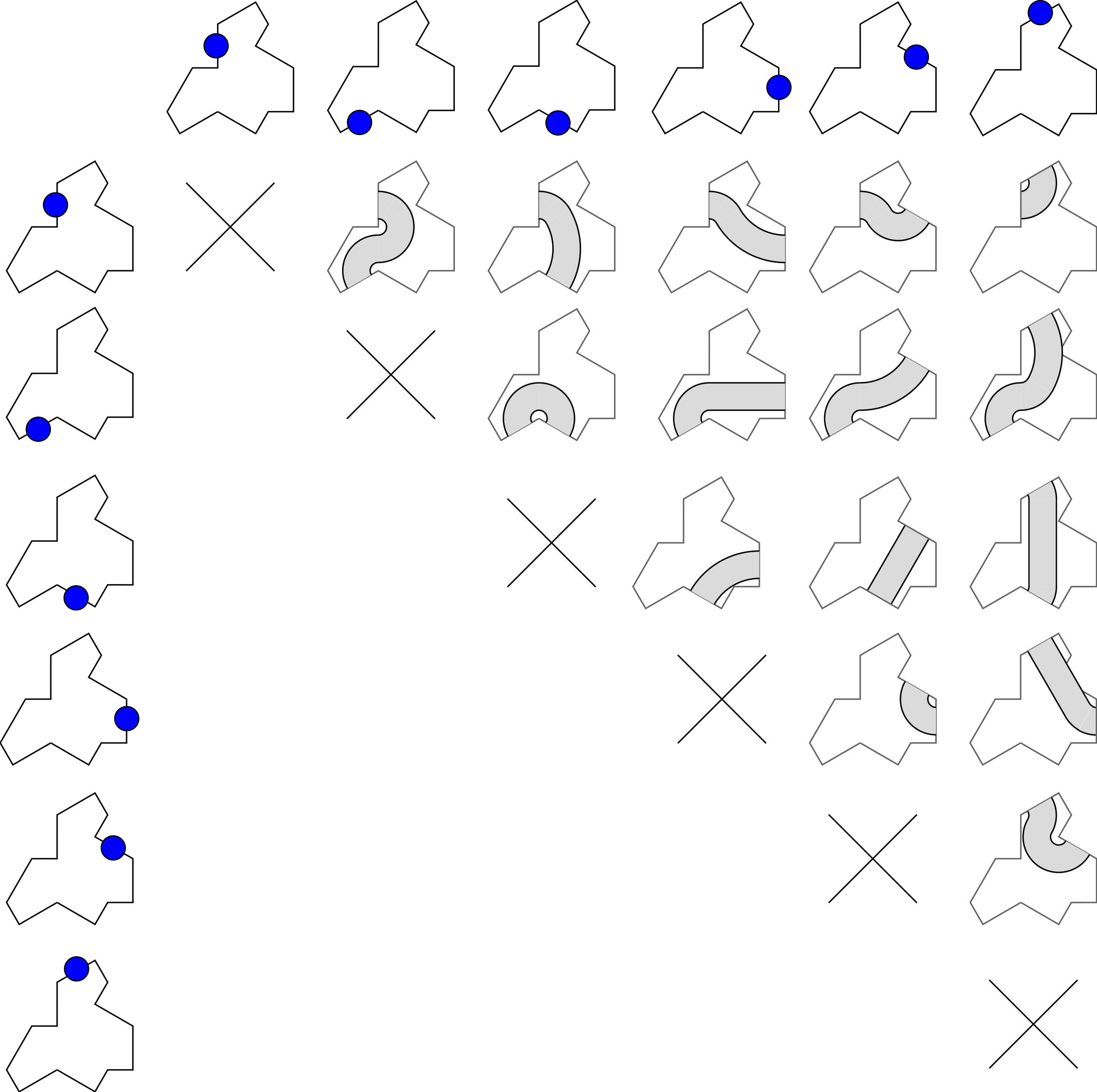
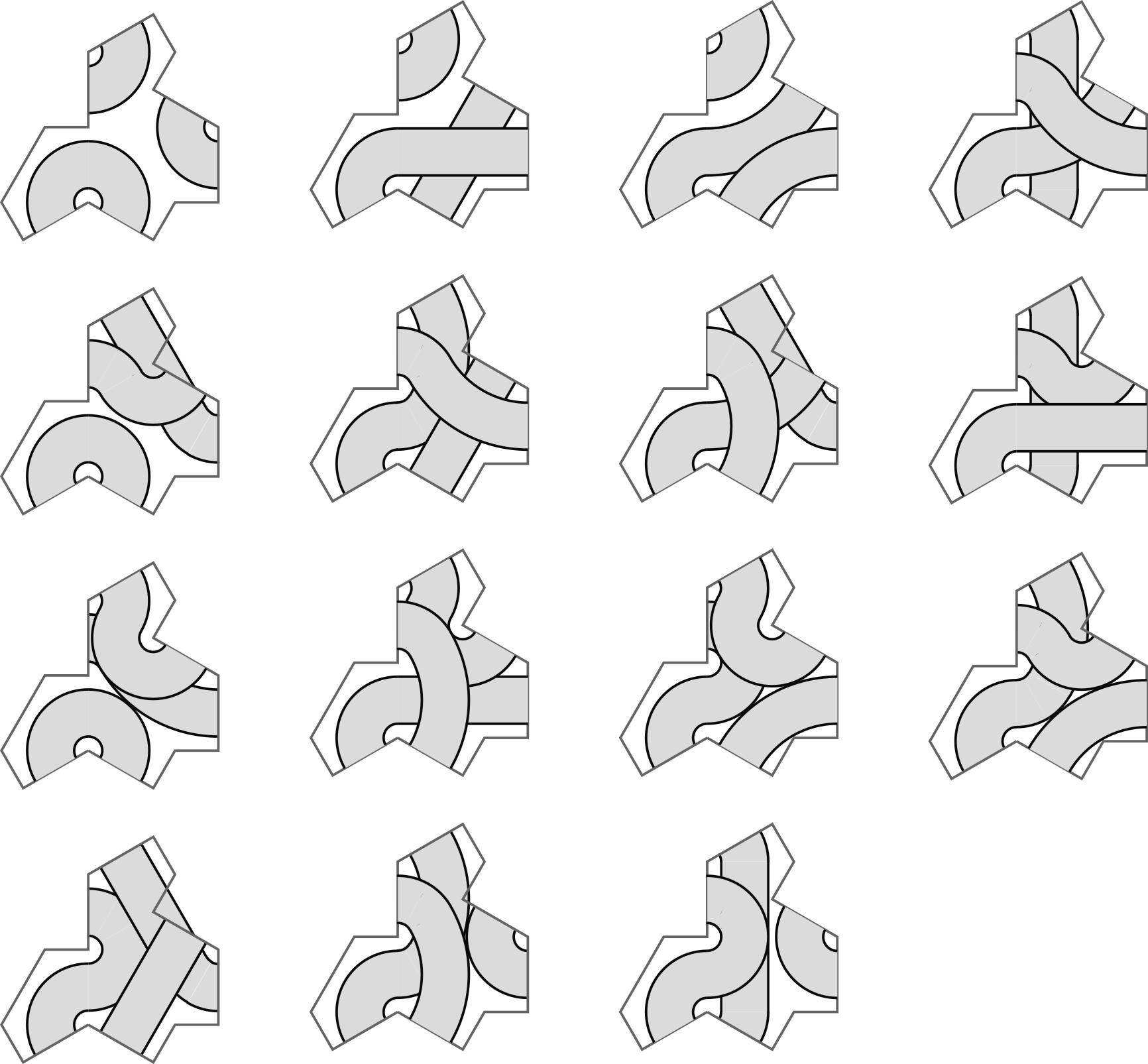
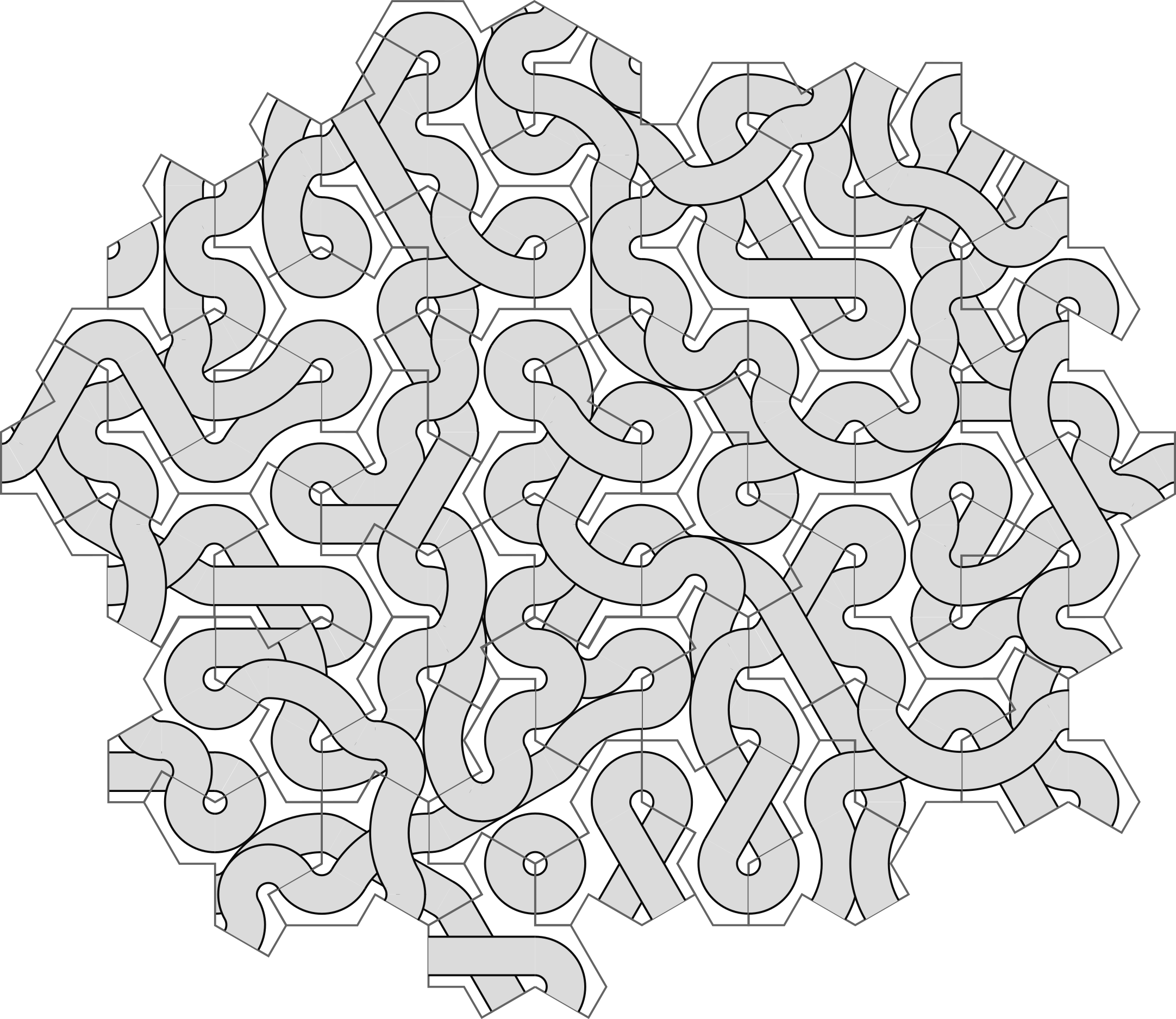
First problem: the tile has 13 sides. So if [...]

---

First published:
February 16th, 2025

Source:
https://www.lesswrong.com/posts/AhmZBCKXAeAitqAYz/celtic-knots-on-einstein-lattice

---

Narrated by TYPE III AUDIO.

---