Evelyn Lamb: Welcome to My Favorite Theorem, joining forces today with Talk Math With Your Friends. I'm Evelyn Lamb. I co-host this podcast. I'm a freelance math and science writer in Salt Lake City, Utah. And this is your other host.
Kevin Knudson: Hi, I'm Kevin Knudson, professor of mathematics at the University of Florida, where it is boiling hot today, and I’m very happy to be in this—how would they put this on on TV?—crossover event, right?
EL: Yeah.
KK: So like, I think last night on NBC, on Wednesday nights, there are all these shows that take place in Chicago: Chicago Med and Chicago PD and Chicago Fire, Chicago Uber, who knows what. Anyway, sometimes they'll just merge them all into one three-hour super show, right? So here we go. This is the math version of this, right?
EL: Yes. And I realized today that our very first episode of My Favorite Theorem, we published that in late July 2017. So this is our early third birthday! And we're so glad that people came to join us! And we are very happy today to have our guest Annalisa Crannell with us. Hi, Annalisa. Can you introduce yourself and tell us a little bit about yourself?
Annalisa Crannell: So hi, my name is Annalisa Crannell. I profess mathematics at Franklin and Marshall College, which is in south-central, southeastern Pennsylvania. It's a small liberal arts college. I got my PhD working in differential equations, partial differential equations, nonlinear differential equations, switched into discrete dynamical systems, topological dynamical systems, but for the past 10 or 15 years have been really thinking hard about projective geometry applied to perspective art.
KK: That’s quite the Odyssey.
AC: Yeah, I was really influenced by by Paul Halmos saying that one of the marks of a really good mathematician is that they can change fields. And so yeah, I feel like I'm trying to enjoy so many different aspects of what this profession allows us to do.
EL: And a fun story, at least it was fun for me, is that one time you were here in Utah giving a talk at BYU, which is down the street. And we went to an art gallery and you pulled out your chopsticks and showed me how you use your chopsticks to help you know where to stand to best appreciate art, and it was just so amazing to me that that was this thing that you could do. So that was that was a lot of fun. And I think it just, to me, sums up the Annalisa experience.
AC: Thank you. Yeah, summing, I guess, is a good thing for mathematicians. I think everybody should carry chopsticks with them. I mean, it's great. It's frugal. It helps you avoid to trash, but it also helps you do really cool mathematics. So what's what's not to love about them?
EL: Yeah. So what is your favorite theorem?
AC: So if you had asked me about five years ago, I would have said the intermediate value theorem. But today, I am going to say no, Desargues’ theorem. So Desargues’ theorem first came into human knowledge in the 1640s. And it's a theorem that sounds like it's sort of about planar geometry, but I really think of it as being about perspective. So is this when I'm supposed to tell you what the theorem says?
KK: Yes, please.
EL: Yeah. Okay, should we all get out our—so this is one, I feel like I always need like a piece of paper. (I’m trying to hold it up, but I’ve got a Zoom background.) But I got my piece of paper out so I can hopefully follow along at home.
AC: Yeah. If you had a piece of paper or a chalkboard right behind you, you could imagine that you would have a triangle, like, standing up on a glass pane. And then on one side of this glass pane would be maybe a magician or somebody holding a light. Maybe your granddaughter drew the magician. (Okay, for people in the podcast, I'm showing a picture that my granddaughter drew on the chalkboard.) If this light shines on the triangle, then it casts a shadow, and the shadow is also a triangle. And so we say those two triangles are perspective from a point, the point is the light source. And we say that because the individual corners, the corresponding corners, are colinear with the light source. So A and the shadow of A are collinear with a light. B and the shadow of B are colinear with a light. But it turns out that those shadows, the triangle and its shadow, are also perspective from a line. And what that means is that if you think not about the points on the triangles, but the three lines on the triangles, and you really think of them as lines, not line segments, so going on forever, then the corresponding lines will also intersect along a line. And you can think of that second line, which we call the axis, as the intersection between the plane of glass that's sitting up in the air and the ground. So the interesting thing to me about Desargues’ theorem is that it pretends like it's a theorem about planar geometry, because this theorem holds when the two triangles are both in the same plane, in R2 or something, but the best ways of proving it, the most standard ways of proving it, are using essentially perspective, going out into three dimensions and proving it for two completely different planes and then pushing them back down into the regular plane. And so to me, this is a really interesting example of sort of how art informs math rather than the other way around. Or maybe they both inform each other.
EL: So going back a little bit, to me when I've I've looked at Desargues’ theorem before, somehow there's this big conceptual leap to me between perspective from a point and perspective from a line. Perspective from a point seems really easy to think about, and perspective from a line, I just have trouble getting it into my brain.
AC: Yeah, I do think perspective from a point is so much more intuitive. And so, so the minorly intuitive, the somewhat intuitive way of thinking of this axis, is you can sort of pretend like it's a hinge. So if these two triangles will sort of fold on to each other from the hinge—the triangle on the glass and the triangle on the ground can fold along this hinge—then they’re perspective from a line. So if you think about something that's in the real world, a flat thing in the real world, and its mirror image, then those two, it's hard to say whether they're perspective from a point, but the lines in the real world thing and the lines in the mirror will intersect along the line where the mirror hits the ground. And so that's that's another way of thinking of this axis, sort of three dimensionally.
KK: So I want to think about this in projective space, which probably isn't correct. Or maybe it is. I don't know. I mean, so these lines are points in projective spaces. This is this, how one might go at this in some other way? I asked the wrong question. I'm sorry.
AC: So that's not exactly the way that I think of it because I think of the line as a line in projective space.
KK: Okay.
AC: And the point is a point in projective space. So the point comes from, you could say, from a one-dimensional line in R-whatever.
KK: Okay.
AC: And so here's one of the interesting things about this theorem and about me loving this theorem. In 2011, one of my coauthors and I wrote a book on the mathematics of perspective art, and we used Euclidean geometry all the way through. We were giving a MathFest mini-course on this and a young mathematician came up to us and said, “I just love how you use projective geometry in art because I learned projective geometry and felt like it had to have something to do with art. And you guys are the ones that explained to me how it does.” And Mark and I turned to each other. We're like, “What kind of geometry?” So neither of us had ever taken a projective geometry class. Neither of us had ever learned any projective geometry. We did not know that it existed. And so this young mathematician ended up changing our lives. We ended up working with her and really learning a bunch of projective geometry in order to come out with our most recent book, which came out last December. And so when you ask questions that get into really deep projective geometry, I'm like, “Ooh, I have to write that one down because that's something else I have to go learn.” So for those of you young mathematicians out there, I just want to say learning new stuff and not knowing stuff is is really so much fun! Don't be afraid of starting something new, even if you don't know it all.
EL: And how did you first encounter Desargues’ theorem?
AC: Oh, man, so I first encountered Desargues’ theorem when, Fumiko Futamura, this young mathematician, had convinced me I needed to learn it. So I bribed an undergraduate to go through Coxeter’s Projective Geometry with me because it seemed like that was the standard book. And Coxeter is, like, the famous guy in this realm, and he is completely non-intuitive. So I found Desargues’ theorem in there, and I'm like, “I have no idea what this means.” The notation is awful. The diagrams are awful. Everything about this is awful. And so I read through his book trying to say, “What does this have to do with art?” And that was a really fun way to read it. So we just decided Desargues’ theorem is about shadows.
EL: Well, I was wondering. So I remember you have also given a talk about squares that kind of blew my mind, where I guess the the thesis of the talk is that all configurations of four points are a square, if you look at it from the right way. Is Desargues’ theorem related to that theorem? I feel like when you said the word shadow that is what reminded me of that other talk.
AC: Yeah, thank you. So that's really cool. So most of us know what the fundamental theorem of calculus says. Most of us know what the fundamental theorem of algebra says. The fundamental theorem of projective geometry in one sense really ought to be Desargues’ theorem. So you can think about these triangles, these points, these lines as objects. For mathematicians, we care about verbs. So a verb is the function. So you can think of a perspective mapping as mapping one set of points and lines to another set of points and lines with this particular rule that says that corresponding points have to line up with the sun, which you call the center, and corresponding lines have to line up with the axis, this hinge. But there's other functions that take points to points and lines to lines. So we know in linear algebra, you can do this all the time, and in linear algebra sets of parallel lines go to other sets of parallel lines. But there's other kinds of functions that do this. They're called colineations. So the fundamental theorem of projective geometry says that if you have four points and their images, and you know that points go to points and lines go to lines, then the entire rest of the function is pre-determined, we know that.
So Desargues’ theorem says that one kind of colineation is perspective mappings, right? Just, like, a shadow or mapping from the floor, this tiled floor onto your canvas through a window. We know from linear algebra, there are these other affine transformations. And so one really cool theorem that I totally love is if you have something that's not a linear algebra one, that's not an affine transformation, then it's automatically a perspective transformation together with an isometry. So you took a photograph and you moved it. That's this notion that every single thing that you do with four points going to four other points that determines a whole function. So yeah, so anytime you have four points connected by four lines, even if they look like a bow tie, or they look like Captain Kirk’s Star Trek logo, it turns out that's actually a weird perspective image of a square moved around somewhere.
EL: And you just have to figure out where you should stand to see it as a square.
AC: Yes, exactly.
KK: Are you guaranteed to be able to—so if it's on the wall, say, could you have to, like, lift it up into a third dimension to be able to see it correctly?
AC: So one of the weird things that happens is if you have a bow tie, we sort of think of a bow tie is that the inside of the bow tie, you would imagine that has to go to the inside of the square. And that is not actually the way it happens. So let's let's think about something that's much more familiar to us. Can you map a circle through perspective into other weird shapes like an ellipse? Well, Sure you can. So imagine that you've got a lampshade, and you've got a circular lampshade, and the shadow that it projects onto the wall is actually a hyperbola. We know that. And the light from the inside of the shadow goes to the part of the hyperbola that goes off towards infinity. Well, if you have the bow tie, think about the area outside of the “x” as almost a hyperbola. So this is when it would be so wonderful if I could actually draw pictures, but it's a podcast. On the on the bow tie, there's two sides that are parallel to each other, and then there's this weird “x” in the middle. The parallel sides, extend them out towards infinity from the bow tie. Right? That turns out to be where the square goes, so if you had a square lampshade, it would cast a shadow that would look like this outside of the bow tie. So the same way that a circular lampshade casts a shadow that looks like the outside of the hyperbola, the U shape of the hyperbola.
KK: My desk lamp is a rectangle, so I’m trying to see if it’s casting the right shadow here.
EL: Yeah, some experiments you can do. I feel like it's this “expand your mind on what a square is” kind of idea.
KK: Got to get rid of those old ideas, man.
EL: Yeah. I know that we we traveled a little bit from Desargues’ theorem and I want to give you a chance to circle back and for me
KK: Or square back. Sorry.
EL: Or square back, or projectively bow tie back to Desargues’ theorem, and I guess what do you love so much about it?
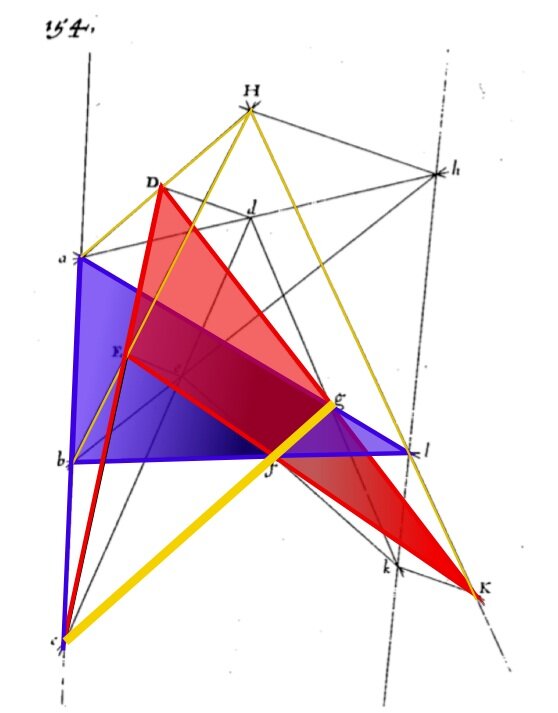
AC: What do I love so much about Desargues’ theorem? One of the things that I love is that it really tightly connects mathematics informing art and art informing mathematics. So Desargues himself, we don't know if he actually wrote this up and published it. We don't have a copy of his original manuscript. We do have something that came out from one of his, sort of acolytes, one of his followers, a guy named Bosse. And if you look at Bosse, okay, to draw Desargues’ diagram, you need 10 points: the three on the first triangle, the three on the second triangle, the sun, that gives you seven, and then the three along the axis. You also need 10 lines: the three on the triangle, the three on the other triangle, the three light rays, that gives you nine, and then the axis. When Bosse first published his diagram, his diagram was incomprehensible. It had 20 lines and 14 points, and it was just really a mess. And it was hard to even figure out where the heck the triangles were.
KK: Yeah, I don’t see them.
AC: And he ended up proving this not using sort of standard geometry, using using numerical stuff called cross-ratios. But the the proofs that make the most sense, that are convincing our proofs that allow us to think about things in three dimensions and use art. So that's one of the cool things, is that actually drawing, if you go and you shade in Bosse’s diagram in a cool artistic way, all of a sudden it sort of pops into 3-d and you can see it, but his original diagram not so much. The same is true of a lot of different proofs. If you try to imagine them as three-dimensional, if you draw them as three-dimensional, the proof becomes more obvious.
But also Desargues’ theorem is actually useful for artists because if you want to draw the shadow of something, if you want to draw the shadow of a kite, if you want to draw a reflection, shadows and reflections, they are projections, so projective geometry, and how do you know how to draw this? You have to use the fact that the shadow or the reflection, or this this projective image, however, you've made it, is perspective from a point and perspective from a line. So you're constantly using Desargues’ theorem to draw these images of images within your image. It just becomes so incredibly useful.
KK: My wife's an artist, but I can't imagine that she would use this. I mean, if you walked up to a typical artist, are they going to say, “Oh yeah, I use Desargues’ theorem all the time?” Or is it just a sort of an intuitive thing where people who are very good at drawing in perspective, can just kind of naturally draw it that way?
AC: Oh, yeah. So the truth is that Desargues’ theorem has really only pretty much been used by mathematicians, and occasionally misused by mathematicians. There's a description in a book by a guy named Dan Pedoe of Desargues’ theorem to draw the image of a pentagon on the top of a square, and he just completely gets it wrong. And Mark and I think that's hilarious. This book has been reproduced zillions of times. Anyway.
So no, actually artists have this incredible skill. One time, we had asked mathematicians and artists at one of our workshops to try to divide the image of a flag into three equal pieces perspectively. So imagine you're drawing the Italian flag going back into the distance, right? How do you do this? In the real world? This there's the three bars are evenly spaced, but in perspective, they're not. And the artists stood up and said, “Well, you just eyeball it, and you just put them here.” And I was horrified. This is not approved. This is not correct. My colleague Mark said, “Okay, this is good. But for those of us who can't just eyeball it, let's see if we can come up with a construction.” And eventually somebody did. They came up with a really cool geometric construction. And Mark had them put this up over the artist’s solution and it was spot on. As a mathematician, I decided to go take an art class. And one of the things we were supposed to do was to draw cans. And so the top of a can is circular, and so the image was going to be an ellipse. And I could not get the proportions right. My ellipses were so awful. So I would say that disarms is an incredibly useful tool for drawing things that look very accurate for people who do not know art, but who are good at math.
KK: Right.
AC: That’s a really long answer to your question. Yeah, artists don't tend to use it, but it really is a useful thing for drawing things that look correct.
KK: Cool. All right.
EL: And you've incorporated this into a class that you teach to help people, I don't know if the purpose of the class is more math or more perspective drawing, but it seems like an interesting mix.
AC: Yeah, we have a course called Perspective and Projective Geometry. We actually have a book that's come out that has Desargues’ theorem right on the cover up there. And it's aimed at the intro to proofs level. So it really teaches students to make conjectures about what they're seeing in the world and then to try to prove those conjectures, but also to try to draw. Ao it's actually sort of an applied course. So they, this students, when we introduce them to Desargues’ theorem, they're actually drawing the shadow of the letter A, and then discovering Desargues’ theorem, and then proving it using many colors and, yeah, lots of cool lines.
It's so much fun! It's a course that really attracts a very unusual swath of students. They all are students who love math, and who are art-curious. Almost none of them are good at art. But I tend to get more women than men in the class. I have often had my class being highly diverse in terms of races and ethnicities. And so for me, it's a fun class. I didn't do it just for the sake of promoting diversity in the math major, but it's sort of unintentionally has done that. And that's a really good feeling.
KK: Very cool. So another thing we like to do on this podcast is ask our guests to pair their theorem with something. So what pairs well with Desargues’ theorem?
AC: Yeah, so I think I already hinted at this, so anything that you can eat with chopsticks goes really well with Desargues’ theorem because chopsticks allow you to have wonderful food and do math at the same time, and what could be better?
KK: So basically, anything you can eat, then, right, you can eat anything with chopsticks?
AC: Soup is a little bit tricky, but yes.
KK: But you drink the soup, right? They give you the chopsticks, you’ve had ramen, right? There's the chopsticks for the noodles.
AC: Yes. Exactly.
EL: Do you have a favorite food to eat with chopsticks?
AC: Oh my goodness. Pretty much everything. I was just realizing ice cream is not so easy with chopsticks.
EL: Yeah.
AC: I think yesterday was national ice cream day. Yeah, I don't I don't know. I take my chopsticks with me in my in my planner bag, and a spoon. And so when I go to restaurants if they try to give me plastic things, I use my chopsticks. So basically, yes, anything I can eat with chopsticks, I will eat with chopsticks. If I can't, I'll use my spoon.
EL: Nice.
KK: We’re getting Thai takeout tonight. Now I'm really excited.
AC: I’m coming to your house.
KK: Sure, come on down. Although you know with all the COVID, I don't think Florida is really a place you want to be coming these days.
EL: So I guess this would be a good time to open the floor to questions. So Brian, I was thinking that I would be able to keep an eye on it, and I totally couldn't. So I'm glad that you were keeping an eye on it. So do you have any questions that our listeners would like to ask Annalisa?
Brian Katz: I’ve noticed three so far. One is from Joshua Holden, would Desargues’ theorem be useful for computer graphics?
AC: That’s a really good question. If I knew anything about computer graphics, I would be able to answer that better. I do know that my students who have gone on into computer engineering tell me that the course that I offered on projective geometry was one of their most useful courses, that this idea of ray tracing was was super, super helpful. So I don't know if Desargues’ theorem itself is specifically useful, but the idea of projective geometry is certainly how we understand the world through videos.
BK: We got a request from Doug Birbrower asking for you to hold up the line drawing while I asked the next one. I was wondering, so when we're talking about triangles, we have these vertices that are special points. How does this idea translate when you're talking about, say, shadows of more complicated objects that might be smooth? You talked a little about circles, but is there a special that happens when you generalize beyond polygons?
AC: One of the things that makes triangles really awesome is the same reason why triangular stools are so useful, is they're always stable, right? Whereas a four legged stool can wobble. If you try to draw the perspective image of an object With four points like a kite, it's really easy to make it be perspective from the sun without being perspective from a line. And if you do something like that, it'll look like maybe the kite is planar, but the shadow is curved, which might make sense on the ground. So in some ways, it's saying triangles really determine planes. Yeah, the question of drawing other curves is really interesting because of how you do or don't define curves in projective geometry. So one way you could think of a curve is a collection of points. You could also think of it as a collection of tangent lines. And so I think a way to generalize Desargues’ theorem to those would be to be talking about those collections of points and those collections of tangent lines.
BK: And then the third one that got some answers in in the chat was: I have a sense that, like, parallel things that when they're prospective from a point that means the point’s at infinity when we're talking about projective geometry. Is their geometric intuition about what it means for the line, perspective from a line, for that line to be infinity? And TJ suggested that it was that the objects are translations of each other.
AC: So if the line is it that that is at infinity, then either you could think of this as being translations, or you can think of it as being a dilation. And so it's a translation if both the axis where the two triangles meet is infinity and the center, that is what how you shine from one to another, is also off at infinity. And they’re are a dilation if the axis is off at infinity, but the center is what we call an ordinary point.
KK: This is new for us, having a Q and A. It's usually just the three of us, you know, me and Evelyn and whoever we're interviewing, but this is fun. I like this interaction.
EL: Yeah, I like that. And people have good questions. Yeah. Great. Thanks. Are there any more questions from the chat that we want to get to? Okay, looks like I'm seeing no. So I think this will sort of wrap up the…oh, Brian. Yeah.
BK: This one just appeared: Do cylindrical polar coordinates throw any light on this?
AC: Oh, so I was just about to say to everybody, “Thank you so much for asking me questions that I actually know the answers to!” And this one, I have no idea. I don't know. I don't know anything about cylindrical polar coordinates. Sorry. Now I'm going to write that one down and go check it out.
EL: But we can all appreciate the “throwing light” phrase of the question. That was very well done. Thank you.
KK: Clever.
EL: So, to wrap up the podcast portion of this, or the the episode with Annalisa portion of this, we will have show notes that are available. Our podcast listeners probably know where to find that at Kevin's website. And on that will include a link to your website, a link to the books that you have. Do you want to say the titles of the books that you've written that people might be interested in?
AC: So the first one, the one from 2011, is called Viewpoints with a subtitle “mathematical perspective, and fractal geometry in art,” and that's suitable for, like, a first-year seminar in math and art. So students don't need to really know anything at all about mathematics. And then the other one is called Perspective and Projective Geometry, and it came out in 2019.
EL: Yeah, so thank you for joining us, Annalisa. And for your doing it in this different fun format.
AC: I’m really flattered that you invited me to do this. Yeah, it's been so much fun trying to think about how to do this without drying gazillions of pictures. I appreciate that.
EL: Yeah.
KK: Thanks so much.
We were delighted to have a crossover event with Talk Math With Your Friends, an online math seminar that runs on Thursdays at 4 pm Eastern time. You can watch a video of this episode, which includes a collection of "flash favorite" theorems from the audience, here. Our guest for this episode was Annalisa Crannell from Franklin and Marshall College, who talked about Desargues' theorem. Below are some links you might find handy after listening to the episode.
Crannell's academic website
Her collaborator Fumiko Futamura's website
Desargues' theorem on Wikipedia, which includes some helpful diagrams
The Image of a Square, a paper about the theorem that every quadrangle is a square if you look at it the right way. (Also available from Futamura's website.)
Viewpoints: Mathematical Perspective and Fractal Geometry in Art by Crannell and Mark Frantz
Perspective and Projective Geometry by Crannell, Frantz, and Futamura
During the episode, Crannell shared Bosse's original diagram for proving Desargues' theorem. It is here. Below is a version of the diagram colored in, making the triangles a little easier to see.